This presentation contains content that your browser may not be able to show properly. This presentation was optimized for more recent versions of Microsoft Internet Explorer.
If you would like to proceed anyway, click here.
Category: Introduction to Biology
Mrs Nerg
| Seven Life Processes | |
| Movement
Reproduction Sensitivity Nutrition Excretion Respiration Growth |
MRS NERG |
| What one MAIN characteristic do ALL organisms have in common? |
|
| They’re all made of cells! | |
Metric Measurement Lab
| Metric Measurement Lab |  |
Part A: Count your drops!
Take a guess – How many drops of water will it take to equal 1 milliliter? _____ drops
Follow the directions to find the number of drops in 1 milliliter of water, then answer the questions. You will need a small graduated cylinder (25 ml), a beaker of water, and an eyedropper for this section. Remember to read the bottom of the meniscus when you are reading the volume of a liquid in a graduated cylinder.
|
 |
| # of drops to 11 ml | # of drops to 12 ml | # of drops to 13 ml | Average |
|
|
Based on your average, how close were you to your guess?________
Based on your average, how many drops would it take to make 1 liter? _______
Part B: Water Displacement
Follow the directions to find the volume of three marbles using water displacement.
- Add 20 ml of water to a 100 ml graduated cylinder. Record this amount in the chart.
- Add three marbles to the cylinder and measure the volume. Record this amount in the chart.
- Find the difference between the two measurements and record in the chart. The difference between the two measurements will be the volume of the three marbles.
| Volume of Water Before adding Marbles (ml) | Volume of Water After Adding Marbles (ml) | Difference in Volume (ml) | Volume of 3 Marbles |
|
|
Part C: Mass Mania
The gram is the standard unit of mass in the metric or SI system. The basic instrument used to measure mass is the mass balance. Some mass measurements can be made using an electronic balance.
|
 |
| Mass of Metric Ruler (g) | Mass of Empty 50-ml graduated cylinder (g) | Mass of 3 Marbles (g) |
|
|
Part D: Volume by Formula
Use the formula to find the volume of the box. Measure to the nearest centimeter before calculating your answer. If necessary, Round your answer to Two Decimal places.
Volume = length x width x height
__________ x __________ x __________ =________________cm3
Part E: Color Challenge
1. Obtain the following items from your teacher:
- 3 beakers with colored water- 25 ml of each color (red, blue, and yellow)
- 1 graduated cylinder (25 ml – 50 ml)
- 1 eyedropper
- 6 test tubes labeled A, B, C, D, E, and F
2. Perform each step outlined below using accurate measurements.
- Measure 17 ml of RED water from the beaker and pour into test tube A.
- Measure 21 ml of YELLOW water from the beaker and pour into test tube C
- Measure 22 ml of BLUE water from the beaker and pour into test tube E.
- Measure 5 ml of water from test tube A and pour it into test tube B.
- Measure 6 ml of water from test tube C and pour it into test tube D.
- Measure 8 ml of water from test tube E and pour it into test tube F.
- Measure 5 ml of water from test tube C and pour it into test tube B.
- Measure 2 ml of water from test tube A and pour it into test tube F.
- Measure 4 ml of water from test tube E and pour it into test tube D.
3. Complete the chart.
| Test Tube | Color | Final Volume (ml) |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
Metric System
The metric system is based on the number 10.
| Main Units of Measurement | ||
| Length | Volume | Mass |
| meter (m) | liter (l) | gram (g) |
Using the above values (meter, liter, & gram) as the base, their value can be increased or decreased by moving the decimal point to the right (lowers the value) or left (raises the value).
Metric Conversion Table |
|||||
| Kilo- (k) |
Base Unit (m, l, g) |
Centi- (c) |
Milli- (m) |
Micro- (µ) |
nano- (n) |
| x 1000 | meter, gram, liter | 100 | 1000 | 1000 | 1000 |
| 1000 | 1 | .01 | .001 | .000001 | .000000001 |
Convert the following values by moving the decimal point the correct number of spaces and in the right direction .
1. 69.8 meters (m) = ________________ centimeters (cm)
2. 152.97 milliliters (ml) = ________________ liters (l)
3. 42.67 liters (l) = _____________ milliliters (ml)
4. 299.32 kilometers (km) = ____________ nanometers (nm)
5. 26 grams (g) = _____________ kilograms (kg)
6. 123.43 centigrams (cg) = ______________ grams (g)
7. 75.2 liters (l) = __________________milliliters (ml)
8. 456.3 grams (g) = ________________ micrograms µg
9. 4507.22 kilometers (km) = _______________millimeters (mm)
10. 0.00297456 kilograms (kg) = ___________ nanograms (ng)
| BACK |
Graph Examples
Examples of Graphs
LINE GRAPHS
A line graph is most useful in displaying data or information that changes continuously over time. The example below shows the changes in the temperature over a week in January. Notice that the title of the graph is “Average Daily Temperature for January 1-7 in degrees Fahrenheit”.
To the left is a table that shows the date in one column and the corresponding temperature in the second column. The line graph on the right shows the degrees of temperature going up the vertical axis (up and down numbers on the left of the graph) and the days of the week on the horizontal axis (going sideways from left to right). The points for the temperature for each day are connected by a line – thus the graph is a line graph.
|
Average Daily Temperature for January 1-7 in Degrees Fahrenheit
|
 |
BAR GRAPHS
Bar graphs are an excellent way to show results that are one time, that aren’t continuous – especially samplings such as surveys, inventories, etc. Below is a typical survey asking students about their favorite after school activity. Notice that in this graph each column is labeled – it is also possible to label the category to the left of the bar. In this case, the numbers for each category are across the bottom of the chart.
A bar chart is marked off with a series of lines called grid lines. These lines typically mark off a numerical point in the series of numbers on the axis or line. In this case, each grid line going up and down marks a multiple of 20 as the graph is divided. More gridlines can make it easier to be exact with the amounts being shown on the bar graph, but too many can make it confusing. Notice that for data that does not fall evenly on a multiple of 20, the bar is in between two grid lines. Bar graphs are useful to get an overall idea of trends in responses – which categories get many versus few responses.
|
Favorite Student After School Activity
|
 |
CIRCLE/PIE GRAPHS
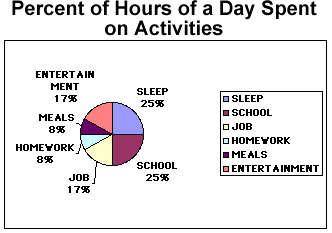
Circle or pie graphs are particularly good illustrations when considering how many parts of a whole are inception. In the table below both the number of hours in a whole day devoted to certain activities is listed as well as the percent of time for each of these activities. The pie chart is then divided very much as a baker’s pie would be into slices that represent the proportional amounts of time spent on each activity.
To the right of the pie chart is a legend that tells which color stands for which category. In addition, the percents are also near the pie slice that stands for that particular amount of time spent.
Percent of Hours of a Day Spent on Activities
| ACTIVITY | HOURS | PERCENT OF DAY |
| Sleep | 6 | 25 |
| School | 6 | 25 |
| Job | 4 | 17 |
| Entertainment | 4 | 17 |
| Meals | 2 | 8 |
| Homework | 2 | 8 |
