|
|
Chromatography of Inks
Introduction:
One of the main jobs of biochemists is to unravel the complexities of chemical compounds and reduce them to their individual components. The term chromatography comes from two Greek words, “chromat” meaning color and the word “graphon” meaning to write. Separation of the components of chemical compounds can be done by using several methods. Liquids can be separate by High Performance liquid Chromatography (HPLC), while the components of gases are separated by Gas Chromatography. Chromatography is a method for analyzing complex mixtures (such as ink) by separating them into the chemicals from which they are made. Chromatography is used to separate and identify all sorts of substances in police work. Drugs from narcotics to aspirin can be identified in urine and blood samples, often with the aid of chromatography.
Chromatography was first used to separate pigments (colors) in leaves, berries, and natural dyes. Paper chromatography is a technique used to separate, isolate, and identify chemical components of a compound. In paper chromatography, the solid surface is the cellulose fibers in the chromatography paper. A solvent or developer (water, alcohol, or acetone) is placed in the bottom of the chromatography chamber. The paper acts as a wick to pull the solvent up the paper. The solvent front will “wick” up the chromatography paper by capillary action. A minute drop of the ink or chemical mixture to be separated is placed near the bottom of the strip of chromatography paper, but slightly above the level of the solvent in the chamber. As the solvent passes over the drop of ink, the components of the ink dissolve in the solvent. Because the components of the ink do not all dissolve at the same rate, as the components of the mixture move upward, they show up as colored streaks. The separated substances on the chromatography paper form a color pattern called a chromatogram.
To determine the rate of migration for each pigment or component of the ink, the Rf value for each pigment must be calculated. The Rf value represents the ratio of the distance a pigment moved on the chromatogram relative to the distance the solvent front moved. Each pigment or compound will have a unique Rf value that scientists can use to identify the substance. The Rf value is calculated using the following formula:
Rf = distance traveled by the compound / distance traveled by the solvent
Objective:
Use the process of paper chromatography to separate the pigments in various markers and then determine the Rf value for each color on your chromatogram.
Materials:
Plastic vials, paper clips, markers in assorted colors, chromatography paper, scissors, pencil
Procedure:
Rf = distance traveled by the compound / distance traveled by the solvent
Data Table 1
|
Color pen/marker used: |
|||
| Separated colors (list top of strip to bottom) |
Distance each color traveled
(mm) |
Distance solvent (H2O) (mm) |
Rf Value for each color
(Distance color traveled / Distance solvent traveled) |
|
Color pen/marker used: |
|||
| Separated colors (list top of strip to bottom) |
Distance each color traveled
(mm) |
Distance solvent (H2O) (mm) |
Rf Value for each color
(Distance color traveled / Distance solvent traveled) |
Questions:
1. Which color of marker did you use?
2. which color separated out first from your ink dot?
3. Why did the inks separate?
4. What was your solvent?
5. If you had used markers that weren’t water-soluble, how would you have had to change this lab?
6. Why did some inks move a greater distance than others?
7. How do scientists use paper chromatography in their investigations?
Identifying Controls and Variables
 Smithers thinks that a special juice will increase the productivity of workers. He creates two groups of 50 workers each and assigns each group the same task (in this case, they’re supposed to staple a set of papers). Group A is given the special juice to drink while they work. Group B is not given the special juice. After an hour, Smithers counts how many stacks of papers each group has made. Group A made 1,587 stacks, Group B made 2,113 stacks. Smithers thinks that a special juice will increase the productivity of workers. He creates two groups of 50 workers each and assigns each group the same task (in this case, they’re supposed to staple a set of papers). Group A is given the special juice to drink while they work. Group B is not given the special juice. After an hour, Smithers counts how many stacks of papers each group has made. Group A made 1,587 stacks, Group B made 2,113 stacks.
|
Identify the:
1. Control Group 2. Independent Variable 3. Dependent Variable 4. What should Smithers’ conclusion be?
5. How could this experiment be improved? |
 Homer notices that his shower is covered in a strange green slime. His friend Barney tells him that coconut juice will get rid of the green slime. Homer decides to check this out by spraying half of the shower with coconut juice. He sprays the other half of the shower with water. After 3 days of “treatment” there is no change in the appearance of the green slime on either side of the shower. Homer notices that his shower is covered in a strange green slime. His friend Barney tells him that coconut juice will get rid of the green slime. Homer decides to check this out by spraying half of the shower with coconut juice. He sprays the other half of the shower with water. After 3 days of “treatment” there is no change in the appearance of the green slime on either side of the shower.
|
6. What was the initial observation?
Identify the- 8. Independent Variable 9. Dependent Variable 10. What should Homer’s conclusion be?
|
Bart believes that mice exposed to microwaves will become extra strong (maybe  he’s been reading too much Radioactive Man). He decides to perform this experiment by placing 10 mice in a microwave for 10 seconds. He compared these 10 mice to another 10 mice that had not been exposed. His test consisted of a heavy block of wood that blocked the mouse food. he found that 8 out of 10 of the micro waved mice were able to push the block away. 7 out of 10 of the non-micro waved mice were able to do the same. he’s been reading too much Radioactive Man). He decides to perform this experiment by placing 10 mice in a microwave for 10 seconds. He compared these 10 mice to another 10 mice that had not been exposed. His test consisted of a heavy block of wood that blocked the mouse food. he found that 8 out of 10 of the micro waved mice were able to push the block away. 7 out of 10 of the non-micro waved mice were able to do the same. |
Identify the- 11. Control Group12. Independent Variable 13. Dependent Variable 14. What should Bart’s conclusion be? 15. How could Bart’s experiment be improved? |
 Krusty was told that a certain itching powder was the newest best thing on the market, it even claims to cause 50% longer lasting itches. Interested in this product, he buys the itching powder and compares it to his usual product. One test subject (A) is sprinkled with the original itching powder, and another test subject (B) was sprinkled with the Experimental itching powder. Subject A reported having itches for 30 minutes. Subject B reported to have itches for 45 minutes. Krusty was told that a certain itching powder was the newest best thing on the market, it even claims to cause 50% longer lasting itches. Interested in this product, he buys the itching powder and compares it to his usual product. One test subject (A) is sprinkled with the original itching powder, and another test subject (B) was sprinkled with the Experimental itching powder. Subject A reported having itches for 30 minutes. Subject B reported to have itches for 45 minutes. |
Identify the- 16. Control Group17. Independent Variable 18. Dependent Variable 19. Explain whether the data supports the advertisements claims about its product. |

Lisa is working on a science project. Her task is to answer the question: “Does Rogooti (which is a commercial hair product) affect the speed of hair growth”. Her family is willing to volunteer for the experiment. |
20. Describe how Lisa would perform this experiment. Identify the control group, and the independent and dependent variables in your description. |
The Hardy-Weinberg formulas allow scientists to determine whether evolution has occurred. Any changes in the gene frequencies in the population over time can be detected. The law essentially states that if no evolution is occurring, then an equilibrium of allele frequencies will remain in effect in each succeeding generation of sexually reproducing individuals. In order for equilibrium to remain in effect (i.e. that no evolution is occurring) then the following five conditions must be met:
Obviously, the Hardy-Weinberg equilibrium cannot exist in real life. Some or all of these types of forces all act on living populations at various times and evolution at some level occurs in all living organisms. The Hardy-Weinberg formulas allow us to detect some allele frequencies that change from generation to generation, thus allowing a simplified method of determining that evolution is occurring. There are two formulas that must be memorized:
p = frequency of the dominant allele in the population
q = frequency of the recessive allele in the population
p2 = percentage of homozygous dominant individuals
q2 = percentage of homozygous recessive individuals
2pq = percentage of heterozygous individuals
Individuals that have aptitude for math find that working with the above formulas is ridiculously easy. However, for individuals who are unfamiliar with algebra, it takes some practice working problems before you get the hang of it. Below I have provided a series of practice problems that you may wish to try out. Note that I have rounded off some of the numbers in some problems to the second decimal place.
PROBLEM #1 You have sampled a population in which you know that the percentage of the homozygous recessive genotype (aa) is 36%. Using that 36%, calculate the following:
PROBLEM #2. Sickle-cell anemia is an interesting genetic disease. Normal homozygous individuals (SS) have normal blood cells that are easily infected with the malarial parasite. Thus, many of these individuals become very ill from the parasite and many die. Individuals homozygous for the sickle-cell trait (ss) have red blood cells that readily collapse when deoxygenated. Although malaria cannot grow in these red blood cells, individuals often die because of the genetic defect. However, individuals with the heterozygous condition (Ss) have some sickling of red blood cells, but generally not enough to cause mortality. In addition, malaria cannot survive well within these “partially defective” red blood cells. Thus, heterozygotes tend to survive better than either of the homozygous conditions. If 9% of an African population is born with a severe form of sickle-cell anemia (ss), what percentage of the population will be more resistant to malaria because they are heterozygous (Ss) for the sickle-cell gene?
PROBLEM #3. There are 100 students in a class. Ninety-six did well in the course whereas four blew it totally and received a grade of F. Sorry. In the highly unlikely event that these traits are genetic rather than environmental, if these traits involve dominant and recessive alleles, and if the four (4%) represent the frequency of the homozygous recessive condition, please calculate the following:
PROBLEM #4. Within a population of butterflies, the color brown (B) is dominant over the color white (b). And, 40% of all butterflies are white. Given this simple information, which is something that is very likely to be on an exam, calculate the following:
PROBLEM #5. A rather large population of Biology instructors have 396 red-sided individuals and 557 tan-sided individuals. Assume that red is totally recessive. Please calculate the following:
PROBLEM #6. A very large population of randomly-mating laboratory mice contains 35% white mice. White coloring is caused by the double recessive genotype, “aa”. Calculate allelic and genotypic frequencies for this population.
PROBLEM #7. After graduation, you and 19 of your closest friends (lets say 10 males and 10 females) charter a plane to go on a round-the-world tour. Unfortunately, you all crash land (safely) on a deserted island. No one finds you and you start a new population totally isolated from the rest of the world. Two of your friends carry (i.e. are heterozygous for) the recessive cystic fibrosis allele (c). Assuming that the frequency of this allele does not change as the population grows, what will be the incidence of cystic fibrosis on your island?
PROBLEM #8. You sample 1,000 individuals from a large population for the MN blood group, which can easily be measured since co-dominance is involved (i.e., you can detect the heterozygotes). They are typed accordingly:
| BLOOD TYPE | GENOTYPE | NUMBER OF INDIVIDUALS | RESULTING FREQUENCY |
|---|---|---|---|
| M | MM | 490 | 0.49 |
| MN | MN | 420 | 0.42 |
| N | NN | 90 | 0.09 |
Using the data provide above, calculate the following:
PROBLEM #9. Cystic fibrosis is a recessive condition that affects about 1 in 2,500 babies in the Caucasian population of the United States. Please calculate the following:
PROBLEM #10. In a given population, only the “A” and “B” alleles are present in the ABO system; there are no individuals with type “O” blood or with O alleles in this particular population. If 200 people have type A blood, 75 have type AB blood, and 25 have type B blood, what are the allelic frequencies of this population (i.e., what are p and q)?
PROBLEM #11. The ability to taste PTC is due to a single dominate allele “T”. You sampled 215 individuals in biology, and determined that 150 could detect the bitter taste of PTC and 65 could not. Calculate all of the potential frequencies.
| Finding Your Genetic Match |
Introduction:
Have you ever noticed that brothers or sisters often look alike? Their inherited traits are what make their physical appearance so similar. An inherited trait is a particular genetically determined characteristic that distinguishes a person. The traits of children are determined by the traits that are passed on from their parents. Some traits are obvious in a family — a child’s nose is shaped like their mother’s nose, but some traits are less obvious. You may have similar traits to many of your classmates even though you are not related to them. Some examples of often un-noticed human traits are the ability or not to roll your tongue, attached or unattached earlobes, dimples or freckles, naturally curly or straight hair, hitchhiker’s or straight thumb, straight or widow’s peak hairline, smooth or cleft chin, or colorblindness or normal vision.
There are numerous traits in humans, but some traits occur more frequently than others. Between 70-90% of the human population have free-hanging earlobes, can roll their tongue, are right-handed, and can taste a chemical called PTC. These traits are called high frequency traits.
Objective:
Students will determine the presence of certain high frequency traits in themselves & their classmates.
Materials:
Genetic Inventory sheet with pictures, paper, pencil, PTC taste strips.
Procedure:
| Human Trait Inventory | |
| Student: | |
| Tongue Roller | |
| Non-Tongue Roller | |
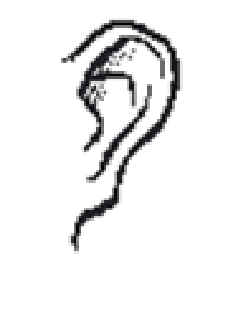
| Attached Earlobes | |
| Unattached earlobes | |
| Dimples | |
| No Dimples | |
| Right-handed | |
| Left-Handed | |
| Widow’s Peak | |
| Straight Hairline | |
| Left Thumb on top when Hands Crossed | |
| Right Thumb on top when Hands Crossed | |
| Hair on mid-digit of hand | |
| No hair on mid-digit of hand | |
| Bent little finger | |
| Straight little finger | |
| Second toe longer than big toe | |
| Second toe not longer than big toe | |
| Can Taste PTC | |
| Can Not Taste PTC | |
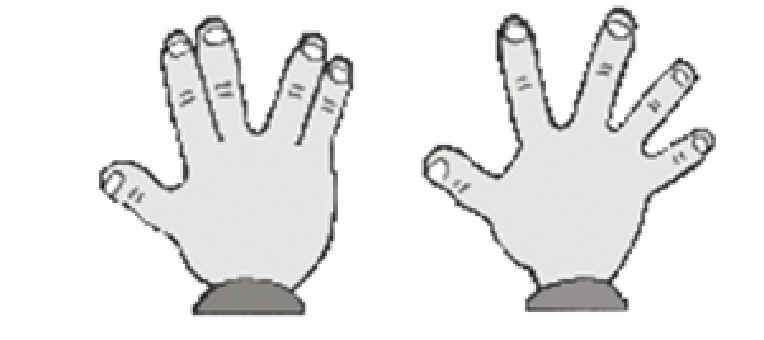
| Vulcan (Fingers spread 2 by 2) | |
| None Vulcan | |
| Class Match: | |
| Tongue Roller | Non Roller | Dimples | No Dimples |
 |
 |
||
| Attached Earlobes | Unattached Earlobes | Widow’s Peak | Straight Hairline |
 |
 |
 |
 |
| Longer Second Toe | Short Second Toe | Bent Little finger | Hitchhiker’s Thumb |
 |
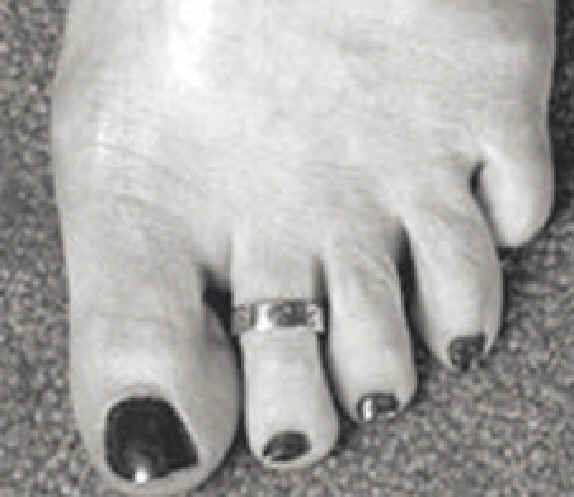 |
 |
 |
| Attached Ear lobes (left) Unattached ear Lobes (right) |
“VULCAN” or No “VULCAN” | Dimples | Right/Left Thumb on top |
  |
 |
 |
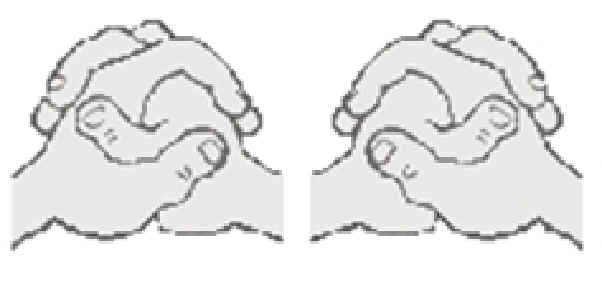 |